本文总结了字牌系列的核心算法，探讨其独特的规则和实现方法。在字牌类棋类游戏中，算法的设计直接影响到游戏的流畅度和公平性。我们将逐步分析各类字牌游戏的关键算法，包括牌型判断、分数计算、出牌逻辑等内容。此外，对优化算法性能的常用方法也进行探讨，以确保在高并发情况下依然保持稳定的用户体验。本总结适合对棋类游戏开发及字牌算法优化有兴趣的读者。
字牌的基本规则不再赘述，详细信息可参考百度百科的“大字牌”页面。
我在这里对字牌游戏进行一个系统分类。我曾参与开发过许多种字牌游戏，涵盖了四川的“贰柒拾”，湖南的“宁乡跑胡子”“湘潭跑胡子”“益阳歪胡子”，以及广西的“八一字牌”“桂林字牌”“全州字牌（四个癞子）”“飞飞字牌（一个癞子）”等。
尽管字牌的玩法多样，但核心流程往往是相似的。所谓核心流程，是指游戏中主要操作流程，如吃牌、碰牌、偎牌、提龙和胡牌等，这些基本流程在不同地区的字牌游戏中都大同小异，差别在于不同地区的术语和表现形式。
但在番型和计分等方面，各地的字牌游戏存在较大差异。例如，有些地区加入了“挡底”“翻神”“翻醒”“八块”等地方性规则。下面是根据玩法相似性和开发复杂度对字牌进行的分类总结：
1. 贰柒拾系列
贰柒拾系列字牌主要流行于四川地区，如“乐山三人”“十四张三人”和“犍为三人”等，随着游戏的扩展，又衍生出二人和四人的玩法。此系列通常按圈数对局，且采用复杂的雨分计算，最佳的计分方案需结合圈数与番型。
玩法难度：★★★★
2. 跑胡子系列
跑胡子系列包含了字牌中衍生更多的玩法，是目前最常见的一类字牌规则体系。此系列的代表有“宁乡跑胡子”“湘潭跑胡子”“常德扯胡子”，广西的一些字牌也归入此类。此系列字牌的挑战主要在于系统操作的丰富性和优先级处理，如出牌、抓牌等。
玩法难度：★★★
3. 鬼胡子系列
鬼胡子主要在湖南的一些地区流行，如沅江、益阳等地。不同于跑胡子系列，鬼胡子的胡牌规则和牌型组合完全不同，计分方式不依赖胡息，且番型复杂多样。
玩法难度：★★★★
虽然跑胡子系列的基础逻辑比其他系列简单一些，但若加入癞子规则，复杂度便会大幅增加。例如，广西的全州字牌设有四个癞子，胡牌方法包含“王闯”“王炸”“王钓”等（即可以任意一张牌胡牌），并需结合翻醒找到好方法，其逻辑复杂度随之上升。
我自主开发了一款APP，涵盖了以上所有字牌玩法，欢迎感兴趣的朋友私信联系，共同学习交流！
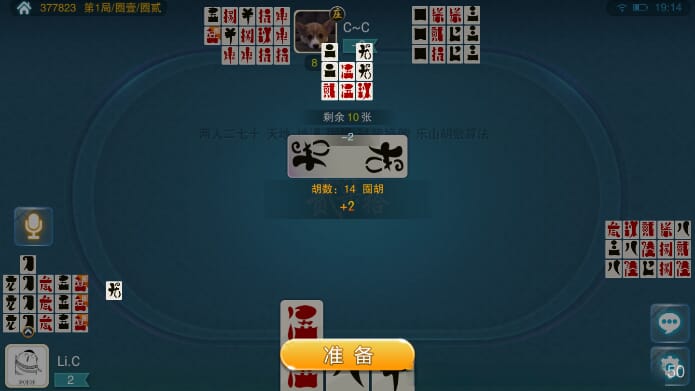
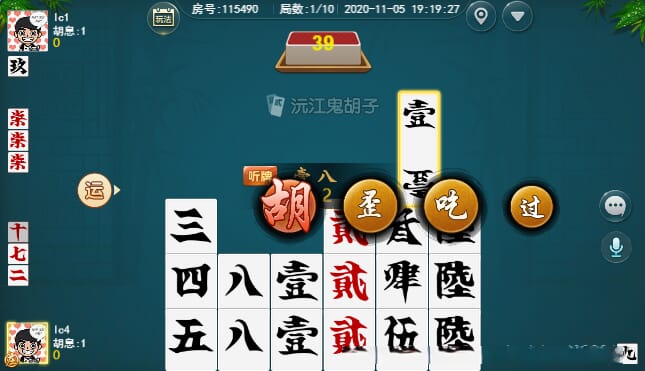
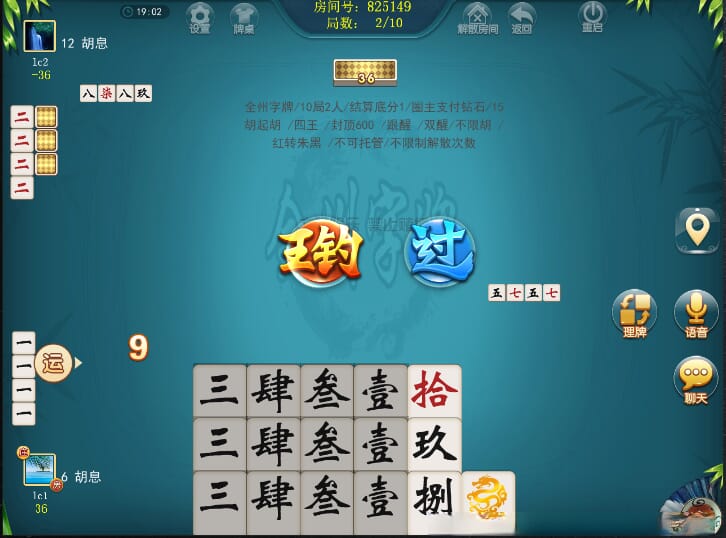
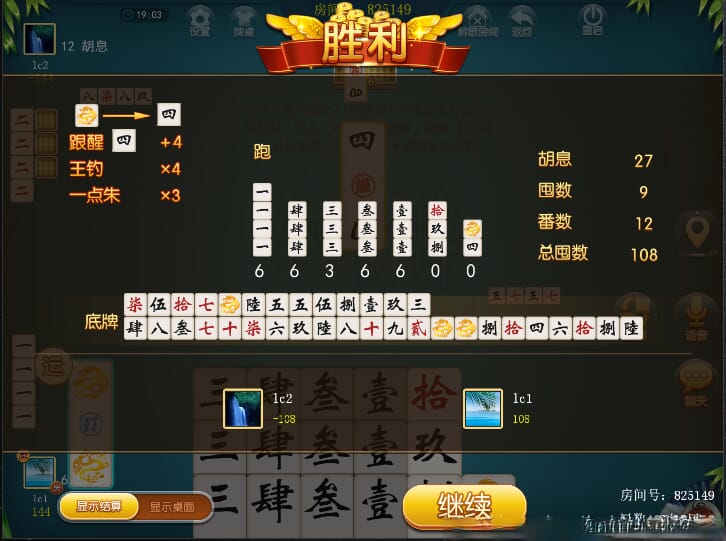
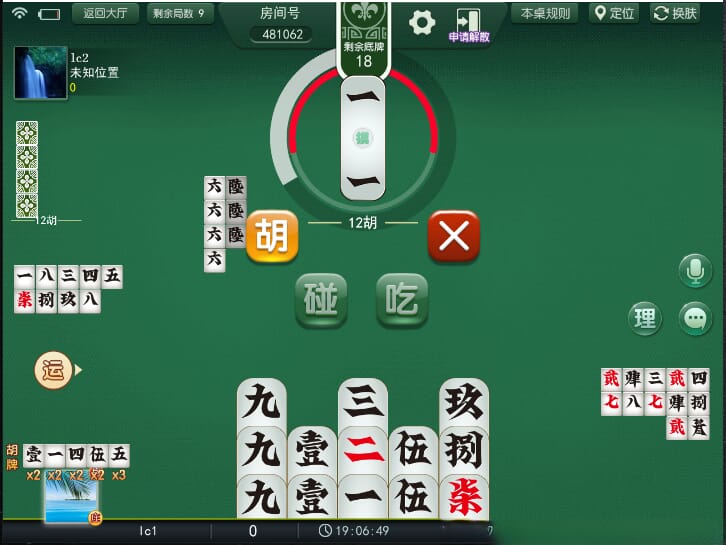
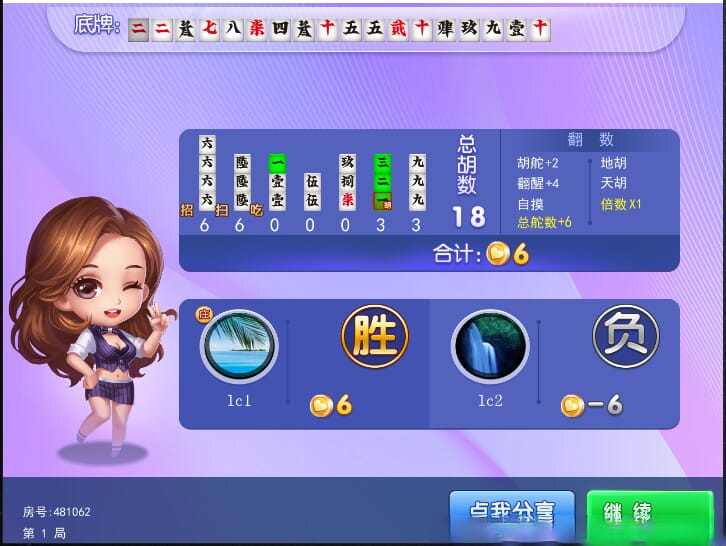
以下是一些牌局中的截图展示，供大家一览，包括牌局中和小结算的画面，截图取自部分字牌APP：
乐山贰柒拾：
鬼胡子：
全州字牌（带癞子）：
桂林字牌：
字牌算法解析
之前曾发布过一篇介绍“贰柒拾”字牌的文章，其中简单提到了胡牌算法。那时，我对字牌算法的理解还只是初步探索。如今，经过多年实践和开发经验的积累，对字牌算法的逻辑与优化有了更全面的认识。接下来，我将深入剖析字牌胡牌算法的核心逻辑。
字牌胡牌的算法主要采用“回溯法”，这种算法极其适合复杂的胡牌玩法，特别是在带有癞子牌的规则下，“多路回溯法”可以显著提升效率。
问题一：回溯法的基本概念是什么？
回溯法是一种递归算法，其核心在于设定条件（比如胡牌的息数），一旦满足条件，就立即停止并返回结果。不同的数据状态共享同样的逻辑，通过尝试不同的路径找到所有可能的胡牌组合。
问题二：为什么选择回溯法？
查表法虽然在麻将等游戏中常用，但由于字牌的胡牌组合过于复杂，构建完整的胡牌表既费时又占用大量内存。而回溯法的灵活性较强，可以动态找到胡牌的最优解，甚至在带有癞子的玩法中，多路回溯法的效果和查表法不相上下。此外，回溯法支持多线程运算，能够分解多个路径，进一步提升了效率。
问题三：如何实现回溯法？
翻到下方，继续了解具体实现步骤。
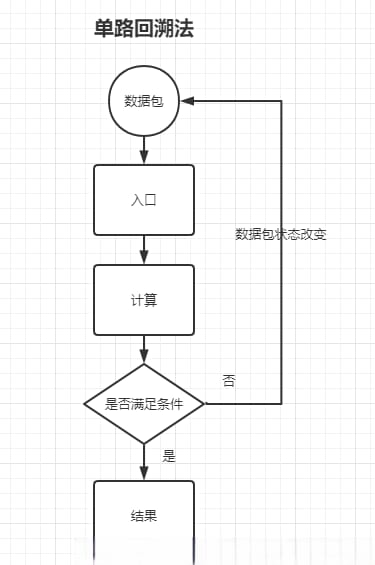
单路回溯法：
单路回溯法的核心在于通过一次回溯计算得出一个最优解，通常是按优先牌型和胡息高低依次处理。由于仅进行一次计算，对方案要求较高。一般情况下，优先大牌型组合，但如果涉及复杂的胡息和番型混合时，单路回溯可能表现不足。在这种情况下，可以构造两个数据包分别进行回溯，并比较结果，这种方式称为“伪多路”（单线程），保持了单路回溯的简洁和效率，又降低了多次计算的负担。
单路回溯法适用于不含癞子的玩法，例如“贰柒拾”和“鬼胡子”系列。在这些玩法中，计算逻辑要求较高。当然也可以将单路回溯强行拆分为多路回溯，但大多数情况没有必要。
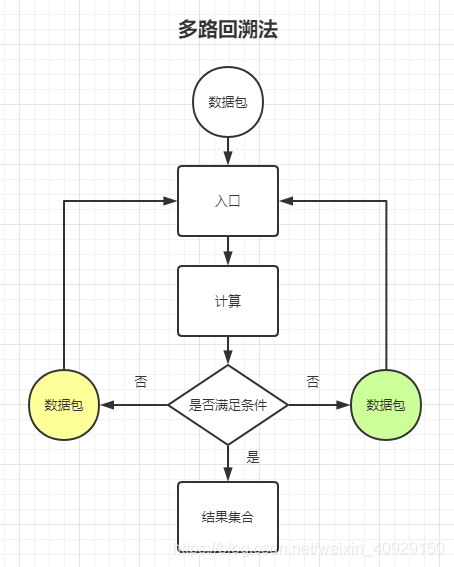
多路回溯法：
多路回溯法则通过并行多次回溯得到所有满足条件的解集。需要注意的是，多路回溯不是简单的多次单路回溯，而是真正的多线程处理。每次回溯计算都无状态处理，数据包只关注自己的计算逻辑，不依赖于其他路径的状态。例如，当一张牌有十种胡牌组合，每种组合需要十次计算，总共有100个数据包，多路回溯能一次性处理多个数据包（多线程），待所有数据包完成计算后再统一筛选最优解。
值得一提的是，单路回溯原则上为单线程，适用于较小的计算负荷或简单的牌型计算，遇到复杂的情况则不适用。而多路回溯法则需借助多线程来提升性能，每个数据包独立运行直到完成所有计算并找到最优解。建议设定最长计算时间，并使用乐观锁机制以确保多线程数据包同步。
回溯法的计算逻辑
无论单路还是多路回溯法，核心仍在于数据的计算过程。好的计算逻辑可显著提升性能，使单路回溯快速得出最优解；而对于多路回溯，全面的计算逻辑能找到所有胡牌组合满足条件。字牌的胡牌判断本质上就是手牌的组合问题，当所有手牌都组合完成，判断是否满足胡牌条件，从而结束计算。以下部分将详细介绍回溯法中“计算”逻辑的具体实现。
计算过程流程图：
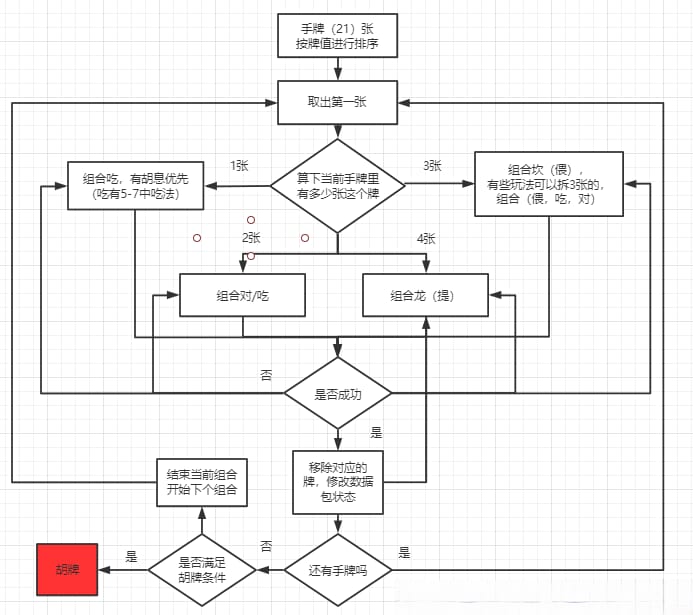
字牌胡牌算法步骤说明
步骤①：
将手牌进行排序，通常按照从大到小的顺序排列。手牌可能包括最后胡的那张牌，也可能不包含，根据情况而定，不一定是21张。此外，已吃、碰、杠的牌不参与计算，但需要累加相应的胡息。
步骤②：
取出第一张牌，判断手牌中该牌的数量。不同的数量对应不同的组合方式。特别要注意，如果这张牌是胡牌，则可能会受到更多限制。
步骤③：
尝试所有可能的组合，优先考虑带有胡息的组合。例如，可以优先尝试2710组合，因为2710带胡息。如果成功，则直接进入下一次回溯，以优先得到最优解。若2710组合不成功，则尝试其他组合方式。
步骤④：
组合成功后，根据组合类型更新当前数据包状态，累加胡息，记录牌型及其他胡牌条件信息，并移除组合所用的牌，递归进入下一次回溯计算。
步骤⑤：
当所有手牌都成功组合后，检查是否满足胡牌条件。若满足，则结束计算并得出胡牌结果。
备注：
此步骤流程适用于跑胡子系列字牌，而对鬼胡子（四张可拆分）或带癞子的玩法，则需要更复杂的计算，但整体逻辑思路相同。
代码示例（JAVA）：
本文主要为理论讲解，实际代码涉及较多逻辑，特别是带癞子的玩法，更需要处理多线程同步和等待。
这里只贴出核心方法，展示基本思路。具体需求可在评论区交流。
Java：
public class HuPaiCalculator {
/**
* 核心胡牌计算方法，适用于无癞子玩法
*/
public boolean calculateHu(List<Integer> handCards, int finalCard) {
// 排序手牌，按从大到小
Collections.sort(handCards, Collections.reverseOrder());
// 将最后的胡牌加入手牌，逻辑根据需求调整
if (finalCard != -1) handCards.add(finalCard);
// 遍历手牌的所有可能组合
return backtrack(handCards, new ArrayList<>());
}
private boolean backtrack(List<Integer> handCards, List<Integer> currentCombination) {
// 所有牌都完成组合
if (handCards.isEmpty()) {
// 判断当前组合是否符合胡牌条件
return checkHuConditions(currentCombination);
}
// 取出第一张牌进行组合
int card = handCards.remove(0);
// 假设尝试2710组合，优先处理大牌组合
if (tryCombination(handCards, currentCombination, card, 2710)) {
return true;
}
// 如果2710不行，尝试其他组合
else if (tryOtherCombinations(handCards, currentCombination, card)) {
return true;
}
// 无法组合，返回失败
handCards.add(0, card);
return false;
}
private boolean tryCombination(List<Integer> handCards, List<Integer> currentCombination, int card, int targetCombo) {
// 判断手牌是否能组成目标组合并递归继续回溯
// 这里需写具体组合逻辑
return false; // 此处为示例，实际逻辑需实现
}
private boolean checkHuConditions(List<Integer> combination) {
// 验证组合是否满足胡牌条件
return true; // 示例返回true，根据实际条件调整
}
}
